By: Brett A. Marmo and Barry J. Carruthers
Xi Engineering Consultants Ltd. Edinburgh, Scotland, U.K.
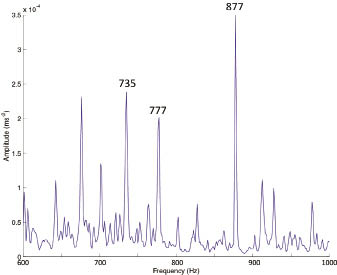
A tower-wall vibration following the yaw test indicates a suite of resonances between 735 and 877 Hz.
Wind turbines occasionally get a bad rap for noise. At times, it’s not the turbine’s fault but rather an internal problem that amplifies the noise. For instance, a recent set of megawatt-scale wind turbines were emitting noise in the 800-830-Hz band. The manufacturer identified 820 Hz as the frequency at which the gear teeth mesh in the gearbox’s last stage. All conventional wind turbine gearboxes have gear-meshing frequencies but do not cause problematic noise, indicating the vibration was being amplified structurally. A vibration survey using a set of accelerometers identified the vibration pathway between the gearbox, nacelle, and tower walls.
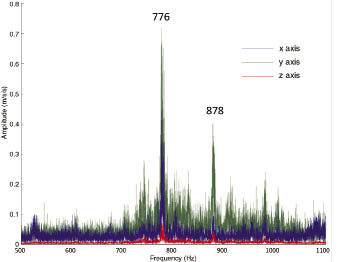
A structural resonance involving the gearbox and its mounts was found in the 776 to 878-Hz band, as were other resonances in a tower wall. A complex dynamic relationship between meshing gear teeth, the gearbox mount, and the tower wall led to the amplification of the gear mesh frequency and the resulting tonal noise. Software such as COMSOL Multiphysics, can assist in identifying the modal shapes of each vibrating element using eigenfrequency and frequency response models. It may be useful to other teams working on turbine noise problems to see how we developed a structural-acoustic interaction model and found solutions to the tonal-noise problem.

Sound pressure levels were measured 20 m from the tower base between 1 and 3,000 Hz. Peaks appear between 700 and 900 Hz, and show good agreement with the vibration survey at site and the eigenfrequency (FEA) analysis of the tower skin.
A vibration survey
First, we initiated a vibration survey used tri-axial accelerometers on the gearbox, generator, yaw bearing, and tower wall. Data was logged at 3,000 Hz and all accelerometers were aligned with the z-axis (up) and x-axis (parallel to the main shaft).
A yaw test excited all resonant frequencies in the structure. The test is akin to a bump test in which a structure is struck with a hammer and the response recorded. However, wind turbines and towers weigh many tons so an acoustic hammer would be too small. Instead, the nacelle is yawed 90° then stopped and the response recorded. The gearbox showed a strong vibration with a band between 720 and 900Hz with peaks at 776 and 878 Hz in the y-direction (transverse to the main drive shaft). This indicates a structural resonance involving the gearbox and its isolation mounts. A suite of resonances were also identified in the tower wall, with the tower skin vibrating at sensor frequencies of 735, 777and 877 Hz.
An active test with the turbine at normal operational speed determined how forced frequencies interact with the structural resonances. Forced frequencies come from some periodic motion, usually mechanical. In turbines, they come from rotor rotation, gear-meshing, and bearings. Waterfall diagrams separate forced frequencies from the structural harmonics of a system. The accompanying waterfall diagram shows a variation of vibration amplitude with frequency (x-axis) and time (y-axis).
High-order structural resonances tend to have complex modal shapes with wavelengths orders of magnitude less than the scale of the entire dynamic structure. While it is possible to interpret the first one or two bending modes and their modal shapes based on data from accelerometers, this becomes increasingly difficult with higher orders because more accelerometers are required.
Gearbox resonance
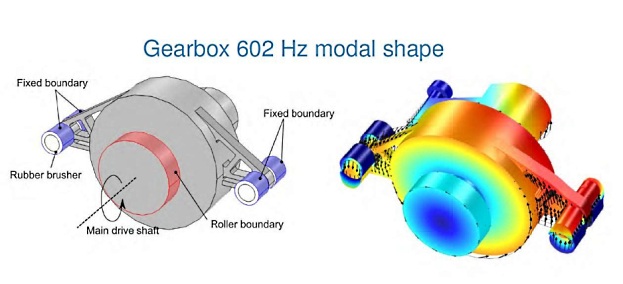
Geometry and boundary conditions (left) were used in the eigenfrequency study. The modal shape of the 792.3 Hz resonance where the colors indicate unitless displacement with red as max.
The gearbox and its bushing mounts were modeled in the FEA program using solid elements. The 11,000-kg gearbox has a moment of inertia, 8.1 kg m2, about an axis co-linear with the main-drive shaft. Rubber bushings isolate the gearbox with a spring constant of 160 kN/mm, which equates to a Young’s Modulus of 43 MPa. The outer boundaries of the bushings were fixed conditions. The main-drive shaft connects to the front of the gearbox prohibiting vertical and horizontal movement but allowing rotation, so roller-boundary conditions were applied to the front of the gearbox. An eigenfrequency analysis found a resonance at 792.3 Hz that involves rotation about an axis co-axial with the main drive shaft. Frequency response analysis later showed that resonance can be excited by frequencies from 720 to 840 Hz. The modal shape and frequency range that excites the resonance is consistent with the data recorded during yaw tests. This resonance involves displacement across the rubber bushings. Hence, their isolating properties are ineffectual in this frequency range letting the 820 Hz gear-meshing pass into the nacelle’s support frame and into the tower.
Sheet metal such as that used in the tower, has what are referred to as skin frequencies. These are high-order bending modes excited when a piece of metal is stuck with a hammer. Skin frequencies, which produce the greatest overall displacement, often cluster around one frequency and combine to produce a distinct note. The tower uses 21-mm thick sheet metal at the base and 10 mm near the top.
A 3D eigenfrequency analysis of the tower uses shell elements. There are two planes of symmetry about the tower’s vertical axis, so it was quartered with symmetric boundary conditions on appropriate edges. The lower (foundation) edge was assigned a fixed boundary condition. Four skin frequencies were found with high participation rates: 727, 763, 799, and 829 Hz. These skin frequencies excite large areas close to the top, thus providing a mechanism to amplify the gear-meshing vibration and transmit it to the surrounding air as noise.
We also developed an acoustic-structural interaction model of the tower walls and air inside and outside the tower. The model combined two acoustic time-harmonic analyses representing internal and external air, which are separated by an axial-symmetric, structural mechanic, harmonic-response analysis that represents the tower wall. A “sound-hard” wall served as the lower boundary condition for the acoustic model inside the tower (the concrete base) and a sound-soft condition worked for the acoustic model outside the tower. The acoustic model of air inside the tower was excited at the upper boundary (bounding the nacelle) with a constant non-zero pressure source. Energy was allowed to propagate through all three models. Tower walls show the resultants.
A remedy for the noise involved breaking the vibration pathway between the gearbox and tower walls. The simplest method was to modify the elastic properties of the rubber bushings used for gearbox isolation so they no longer participate in resonances close to 820 Hz and thereby cease allowing passage of gear-mesh vibration. However, due to constraints, such as a required stroke length, it was impractical to either sufficiently stiffen or soften the bushings. Instead, resonance in the tower skin was modified. Tower skin has a high Q-factor (about 200, equivalent to a loss factor of 0.0025) which is why it rings so effectively. To reduce the amplification effect of the tower skin in the 720 to 830 Hz range, we selected a thin composite laminate with high-loss factor damping (0.09) to apply to the turbine walls. Eigenfrequency models identified significant amplification between the 3rd and 8th weld. The acoustic-structural interaction model was modified to examine the effects of covering different parts of the tower. A 3-mm thick section of damping material with appropriate elastic parameters and a damping factor of 0.09 was placed on the tower wall. The comparison of damped tower sections shows the sound pressure level 20 m from the base of the tower for models with different amounts of damping laminate. After a cost-benefit analysis, the turbine manufacturer was able to choose the minimal amount of damping laminate to install for satisfactory reduction in noise levels.
This wind project demonstrated several uses of the software. Eigenfrequency analysis complimented data collected in a vibration study and allowed determining complex modal shapes of high-order resonances. Models showed gear-teeth vibrations moving from gearbox, through isolators, and into the tower wall. Once the models provided understanding of the modal shapes of the amplifying skin frequencies, it was possible to target areas close to the top of the tower with a damping laminate. Finally, the software helped develop an acoustic-structural interaction model that showed how different amounts of coverage with the damping laminate affected the sound level outside the tower. This model let the turbine OEM select a cost-effective solution which satisfied regulatory requirements and allowed the continued operation of the wind turbines without impinging on residential communities. WPE
Filed Under: Software